Get unique random numbers in C#

The source code this blog mentioned is here: https://github.com/Anduin2017/SuperRandom

The traditional methods for obtaining `n` non-repeating random numbers are:

• The random number is generated by the linear congruence method, and each random number is generated and compared in the database. If it already exists, the number is discarded.
• Randomly generate a linear sequence, and then shuffle the sequence.

The time complexity of the above traditional method is `O (n ^ 2)`. Especially in the case of larger data, for the first algorithm: after the generation of a large number of numbers already exists, the performance will become slower and slower. For the second method, it will take up a very high memory space.

My solution is based on the RSA algorithm, whose time complexity is `O (n)` and space complexity is `O (1)`. It is only linearly related to the number of random numbers required and does not need to be compared with any data set. So the performance is fast. Especially when it is over one million, it is obviously superior to any random number algorithm that depends on storage.

N is a positive integer.
Let a positive integer A be distributed in the set [2, (N-1)]
C = (A ^ D) mod N
And meet the following conditions:

D is prime
N is the product of two prime numbers (P, Q)
P! = Q
(D * E) mod ((P-1) * (Q-1)) = 1

∵ C = (A ^ D) mod N
∴ A = (C ^ E) mod N
∴ C and A are one-to-one mapping
∵ A is distributed in the set [2, (N-1)]
∴ A does not repeat, no omission
∴ C does not repeat, no omission

First, we gonna build a simple prime detect method:

        public bool IsPrime(int input)
        {
            var testSize = Math.Sqrt(input);
            for (int i = 2; i <= testSize; i++)
            {
                if (input % i == 0)
                    return false;
            }
            return true;
        }

And a method that returns a prime sequence:

        public IEnumerable<int> PrimeNumbers()
        {
            yield return 2;
            for (int i = 3; true; i += 2)
            {
                if (IsPrime(i))
                {
                    yield return i;
                }
            }
        }

A method to detect if the value of E is correct:

        public bool IsValidE(int d, int e, int p, int q)
        {
            return (d * e) % ((p - 1) * (q - 1)) == 1;
        }

So we can find a valid E from natural numbers:

        public IEnumerable<int> GetNaturalNumbers()
        {
            for (int i = 0; true; i++)
            {
                yield return i;
            }
        }       

        public bool HaveValidE(int d, int p, int q, out int e)
        {
            foreach (var naturalNumber in GetNaturalNumbers())
            {
                if (naturalNumber > d * (p - 1) * (q - 1))
                {
                    break;
                }
                if (IsValidE(d, naturalNumber, p, q))
                {
                    e = naturalNumber;
                    return true;
                }
            }
            e = 0;
            return false;
        }

Before we can get the E, we need p and q calculated.

P and Q are two primes in which multis values the input N. Just write a method to break N to P and Q.

        public bool TryBreakNumber(int x, out int left, out int right)
        {
            if (IsPrime(x))
            {
                left = right = 0;
                return false;
            }
            var testMax = Math.Sqrt(x);
            foreach (var leftPrime in PrimeNumbers())
            {
                if (leftPrime > testMax) break;
                var rightPrime = x / leftPrime;
                if (leftPrime * rightPrime == x && IsPrime(rightPrime))
                {
                    left = leftPrime;
                    right = rightPrime;
                    return true;
                }
                else continue;
            }
            left = right = 0;
            return false;
        }

And get valid D and E from Q and P.

        public (int d, int e) GetDAndE(int p, int q)
        {
            foreach (int d in PrimeNumbers())
            {
                if (HaveValidE(d, p, q, out int e))
                {
                    return (d, e);
                }
            }
            throw new InvalidOperationException("WTF!");
        }

Now that check if what we got from those methods is valid.

        public bool TryGetRSAParameters(int n, out int p, out int q, out int d, out int e)
        {
            p = 0;
            q = 0;
            d = 0;
            e = 0;
            if (IsPrime(n))
            {
                return false;
            }
            if (!TryBreakNumber(n, out p, out q))
            {
                return false;
            }
            if (p == q)
            {
                return false;
            }
            (d, e) = GetDAndE(p, q);
            return true;
        }

That function returns true if it can get correct p, q, d, and e. And returns false when failed.

To get our final random sequence, just call I ^ d % N.

        public static IEnumerable<int> GetRandomNumbersRaw(int n, int d)
        {
            for (int i = 2; i < n; i++)
            {
                var mod = BigInteger.ModPow(BigInteger.Pow(i, d), 1, n);
                yield return (int)mod;
            }
        }

As I mentioned, the input N might not be valid. We need to skip all invalid inputs and find the nearest N around it.

        public IEnumerable<int> GetRandomNumbers(int max)
        {
            int n, d;
            for (n = max + 2; !TryGetRSAParameters(n, out int p, out int q, out d, out int e); n++)
            {
            }
            return GetRandomNumbersRaw(n, d)
                .Select(t => t - 2)
                .Where(t => t < max);
        }

Now everything is done. This method returns all valid random numbers.

Test it in your Main method.

static void Main(string[] args)
{
    while (true)
    {
        Console.WriteLine("How many unique random numbers do you want?");
        if (!int.TryParse(Console.ReadLine(), out int counts))
        {
            break;
        }
        var array = new int[counts];
        foreach (var rand in new Randomizer().GetRandomNumbers(counts))
        {
            Console.WriteLine("Got random number: " + rand);
            array[rand] += 1;
        }
        foreach (var bit in array)
        {
            if (bit > 1)
            {
                Console.WriteLine("Bit set twice! Wrong code!");
            }
            if (bit < 1)
            {
                Console.WriteLine("Bit not set! Wrong code!");
            }
        }
    }
}

Outputs demo:

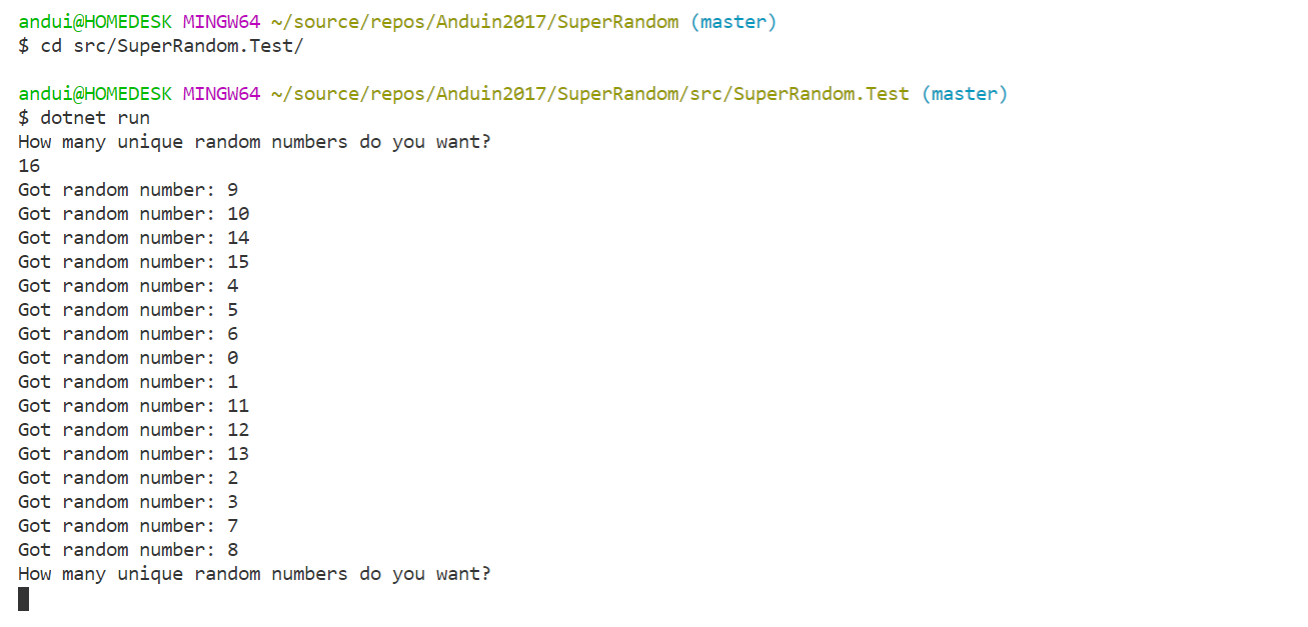
Very random, and unique. Cool!