复习数据结构 - 撸个哈希树

闲来无事，没事儿消遣。如何写一个插入、查找、删除的时间复杂度都是 O(1) 的集合呢？

当然我知道肯定是个人都会立刻反应：直接用 Dictionary！嗯……当然可以。用 HashSet 也不错。

不过，我们给自己限制限制，来增加难度。如果纯手撸，不用任何库，怎么撸一个 O(1) 的集合呢？

直接把输入的内容哈希一下，拿哈希，二分索引，不就完事儿了？属于简单题。花10分钟撸了一个，以便后人吐槽。

public sealed class BinaryHashTrie
{
    private BinaryHashTrie? _left;
    private BinaryHashTrie? _right;
    private bool _isTerminal;

    private bool ExistsBin(int hash)
    {
        if (hash == 0)
        {
            return _isTerminal;
        }

        var goLeft = (hash & 1) == 0;
        var next = hash >> 1;
        return goLeft 
            ? (_left?.ExistsBin(next) ?? false)
            : (_right?.ExistsBin(next) ?? false);
    }

    private BinaryHashTrie AddBin(int hash)
    {
        if (hash == 0)
        {
            _isTerminal = true;
            return this;
        }

        var goLeft = (hash & 1) == 0;
        var next = hash >> 1;
        if (goLeft)
        {
            _left = _left == null ? new BinaryHashTrie() : _left.AddBin(next);
        }
        else
        {
            _right = _right == null ? new BinaryHashTrie() : _right.AddBin(next);
        }
        return this;
    }
    
    public void Add(string input)
    {
        var hash = Math.Abs(input.GetHashCode());
        AddBin(hash);
    }

    public bool Exists(string input)
    {
        var hash = Math.Abs(input.GetHashCode());
        return ExistsBin(hash);
    }
}

用法：

        var myDic = new BinaryHashTrie();
        myDic.Add("Java");
        myDic.Add("Python");
        myDic.Add("C++");
        myDic.Add("C");
        for (var i = 0; i < 10000000; i++)
        {
            // Add a random string
            myDic.Add("RandomString" + i);
        }
        myDic.Add("CSharp");

        Console.WriteLine("Exists: CSharp " + myDic.Exists("CSharp"));
        Console.WriteLine("Exists: Java " + myDic.Exists("Java"));
        Console.WriteLine("Exists: C++ " + myDic.Exists("C++"));
        Console.WriteLine("Exists: Ruby " + myDic.Exists("Ruby"));
        Console.WriteLine("Exists: Rust " + myDic.Exists("Rust"));

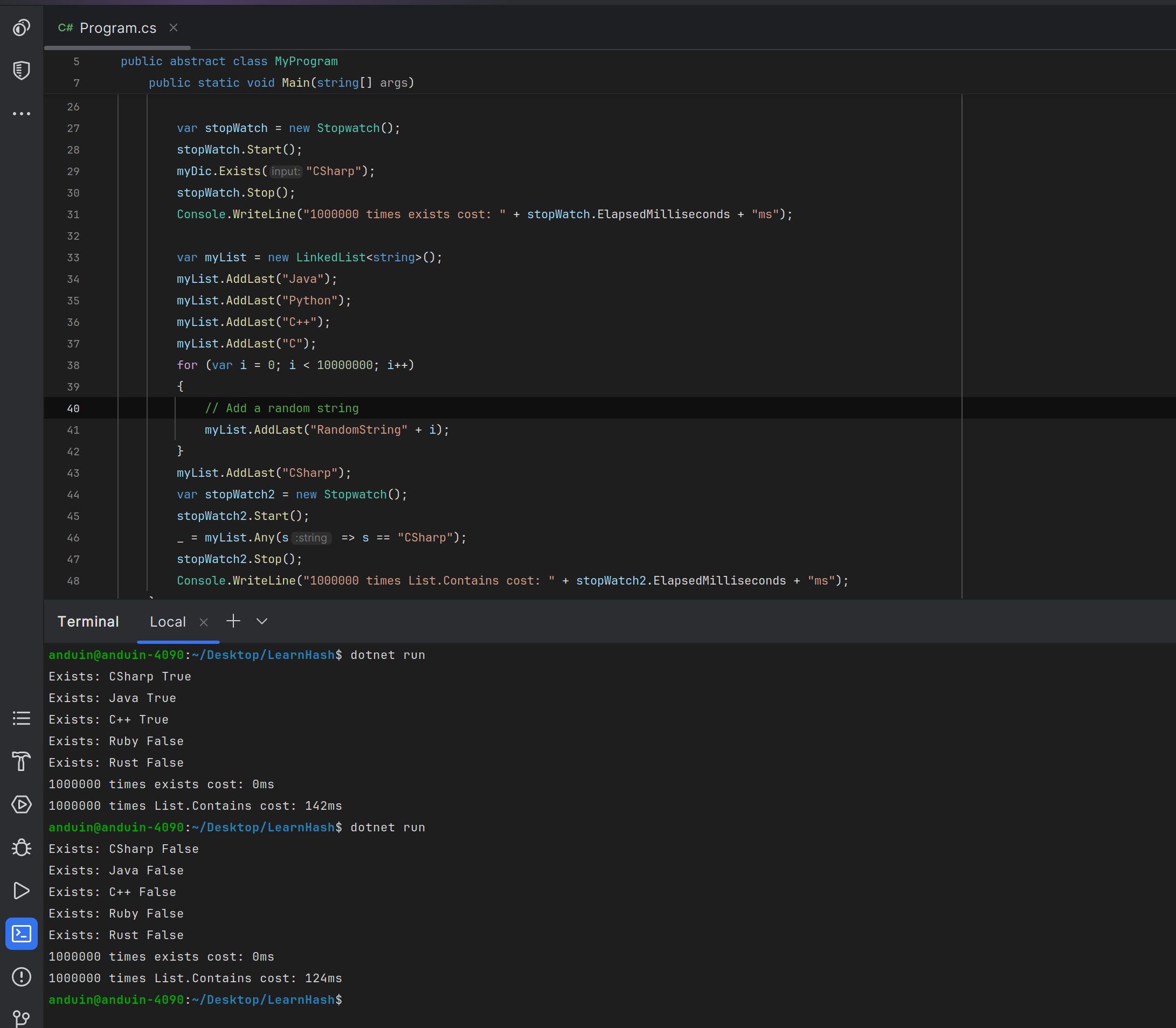
当然我实际跑了一下，显然这玩意儿肯定比链表快多了。时间复杂度控制在 O(1)。当然它的问题就是可能会发生哈希碰撞。所以结果有出错的概率（误判将不存在的string判断为存在）。适合做低精度场景下的加速，比如判断用户是否已注册。